Telusko Docs

What Is a Factorial?

The factorial of a positive integer n (denoted as n!) is the product of all positive integers from n down to 1.

Example:

5! = 5 × 4 × 3 × 2 × 1 = 120

Mathematically, a factorial is defined as:

n! = n × (n − 1)!
Base case: 1! = 1

Why Recursion Fits Factorial

Recursion is well-suited for factorial because:

The factorial of a number depends on the factorial of the previous number.
The problem naturally breaks into smaller sub-problems, and each step depends on the result of the previous step
The recursive definition directly mirrors the mathematical formula.

Recursive Breakdown of Factorial

For 5!, the recursive flow looks like this:

5! = 5 × 4!
4! = 4 × 3!
3! = 3 × 2!
2! = 2 × 1!
1! = 1   ← Base Case

Each step reduces the problem until it reaches the base case (1!).

Recursive Factorial Function

Every recursive solution must include:

1. Base Case Stops the recursion and prevents infinite calls

if num == 1:
    return 1

2. Recursive Case Calls the function with a smaller input

return num * fact(num - 1)

Python Implementation

def fact(num):
    if num == 1:
        return 1
    return num * fact(num - 1)

result = fact(5)
print(result)

Output:

How the Call Stack Works

The call stack is a memory structure that keeps track of active function calls in a program. In recursion, it plays a crucial role in managing repeated function calls.

Call_Stack_in_Python

What Happens When a Function Is Called

Each time a function is called, Python creates a new stack frame.
This frame stores:
- Function parameters
- Local variables
- The point to return to after execution
The frame is pushed onto the call stack.

Call Stack in Recursive Functions

In recursion, a function keeps calling itself.
Each recursive call is added on top of the previous one in the stack.
This continues until the base case is reached.

Reaching the Base Case

The base case (fact(1)) stops further recursive calls.
It returns a value (here, 1) to the previous function call.

Unwinding the Call Stack

After the base case returns, the stack starts unwinding.
Each function:
- Resumes execution
- Uses the returned value
- Computes its result
- Returns to the caller

Return order:

fact(1) → 1
fact(2) → 2 × 1 = 2
fact(3) → 3 × 2 = 6
fact(4) → 4 × 6 = 24
fact(5) → 5 × 24 = 120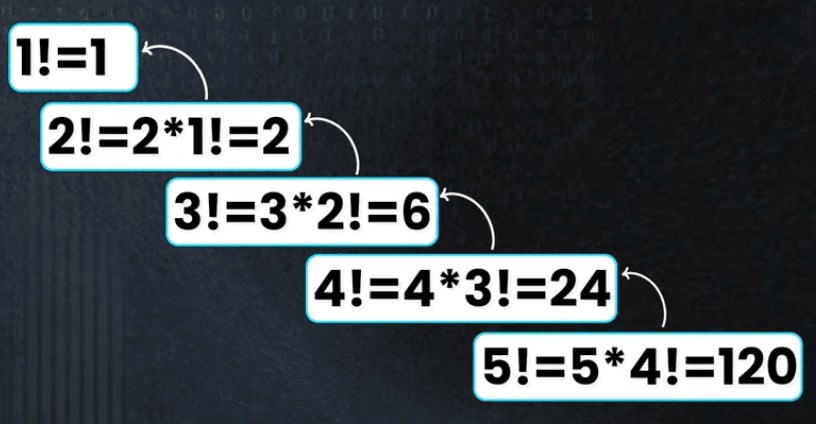

Call_Stack_Call

Stack Overflow and Recursion Limits

If recursion goes too deep without a proper base case:
- The call stack grows excessively
- Python raises a RecursionError
This protects the system from memory exhaustion.

Summary

Factorial can be implemented using recursion by reducing the problem size.
The base case 1! = 1 prevents infinite recursion.
Recursive calls build a call stack and resolve in reverse order.
The recursive approach offers clarity and aligns well with the mathematical definition.

Written By: Muskan Garg

Factorial Using Recursion