Factorial

▶

What is a Factorial?

The factorial of a non-negative integer n, written as n!, is the product of all positive integers from 1 to n.

Example:

5! = 5 × 4 × 3 × 2 × 1 = 120

Mathematical Definition

For any integer n ≥ 1:

n! = 1 × 2 × 3 × ... × n

Special case:

0! = 1

Factorial is a fundamental mathematical concept that helps build logical thinking and is widely used in programming to understand loops, functions, and recursion.

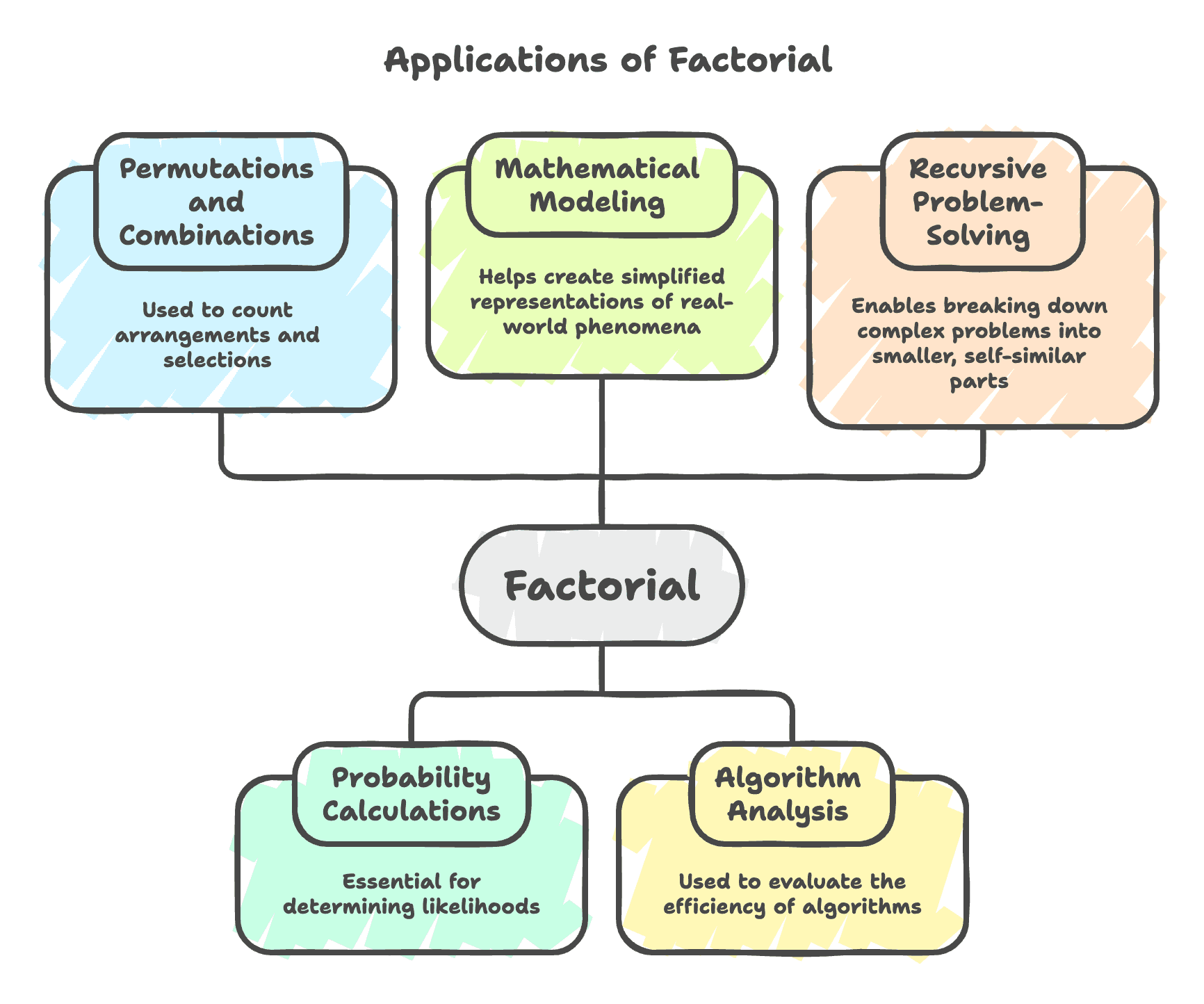
Why Factorial is Important in Programming?

• Strengthens understanding of loops and iteration
• Acts as a stepping stone to recursion
• Commonly used in combinatorics, probability, and algorithm design
• Demonstrates how programs handle large numbers

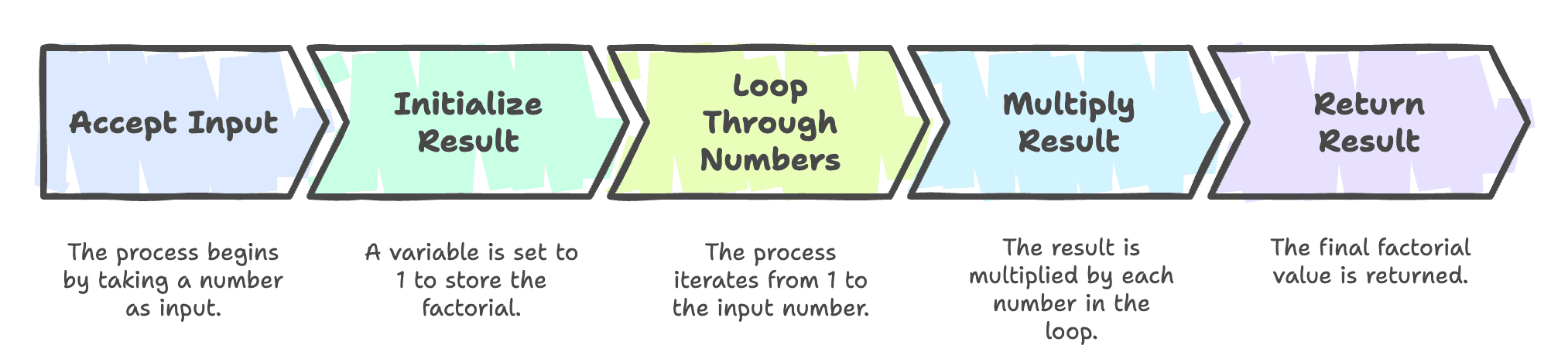
Implementing Factorial Using a Loop (Iterative Approach)

Step-by-Step Logic

1. Accept a number num as input.
2. Initialize a result variable (res) to 1.
3. Loop from 1 to num (inclusive).
4. Multiply res by each number in the loop.
5. Return the final result.

Example

def fact(num):
    res = 1
    for i in range(1, num + 1):
        res = res * i
    return res

result = fact(5)
print(result)

Output:

120

Here,

• res = 1 Initializes the accumulator for multiplication.

• range(1, num + 1) Ensures all numbers from 1 to num are included.

• res = res * i Continuously multiplies values to build the factorial.

More Examples

print(fact(12))

Output:

479001600

Handling Large Factorials in Python

• Factorials grow very rapidly (non-linear growth).

• Example:

  20! = 2,432,902,008,176,640,000

• Python supports arbitrary-precision integers, so it can handle very large factorials such as 100! or even 1000!.

• However, extremely large factorials may consume significant memory and time, depending on system limits.

Summary

• Factorial multiplies all positive integers up to a given number.
• It can be implemented easily using a for loop.
• Python handles large factorials efficiently due to dynamic integer sizing.
• Factorial is foundational for understanding loops, functions, and recursion.
• Widely used in mathematics and real-world programming problems.